nMeas (1/f) - A modular kit of hard- and software for noise measurements. "1/f noise edition"
Features:
- ...
- ...
- ...
Measuring noise and verifying/interpreting the results requires some in-depth knowledge, which is
not available on these pages.
Here are a few, unsorted and short suggestions for introductory reading about noise, noise measurement, FFT and more...
- AppNote (National)Noise Specs Confusing?
- AppNote (TI): "Noise Analysis in OPs"
- AppNote (Analog)Op Amp Noise Relationships: 1/f Noise, RMS Noise, and Equivalent...
- AppNote (National)Super Matched Bipolar...
- Ron Mancini (TI): OpAmps for Everyone
- Jim Williams (Linear): 775nV Noise Measurement...
- Art Kay (TI): Analysis and Measurement of Intrinsic Noise in Op Amp Circuits (no direct link)
- Don LaFontaine (Intersil): ... Accurate Voltage and Current Noise Measurements...
- Smith/Sheingold (Analog)Noise and Operational Circuits
- Boggs/Doak/Walls (NIST)Measurement of Voltage Noise in Chemical Batteries
- ...more to come...
===
(*1*) If you never heard about anything like "voltage noise", "current noise", "equivalent noise bandwidth",
"noise power" (and much more), you'll probably won't need "nMeas" ;-)
Preface
The complete designed focused on
- minimal part count
- standard components
- easy setup (*1*)
- practical measurements
- (... some more I forgot ...)
===
(*1*) Except for adjusting the 20-60dB amplifier. This might requires some pricey helpers...
(*2*) typically below -180dBVrms/sqrt(Hz)
The nMeas (1/f) Kit
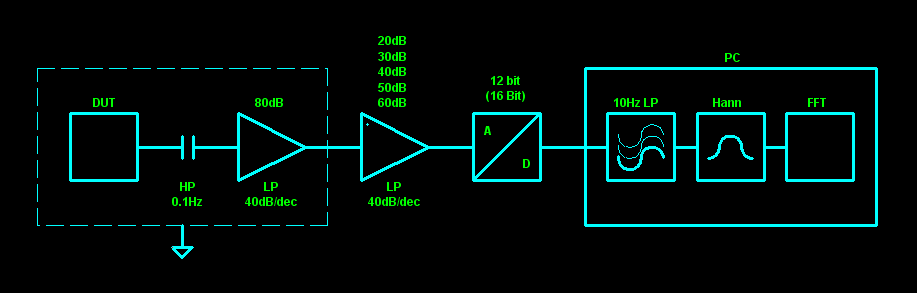
Hardware
The Cookie Box (nMeas-PRE)
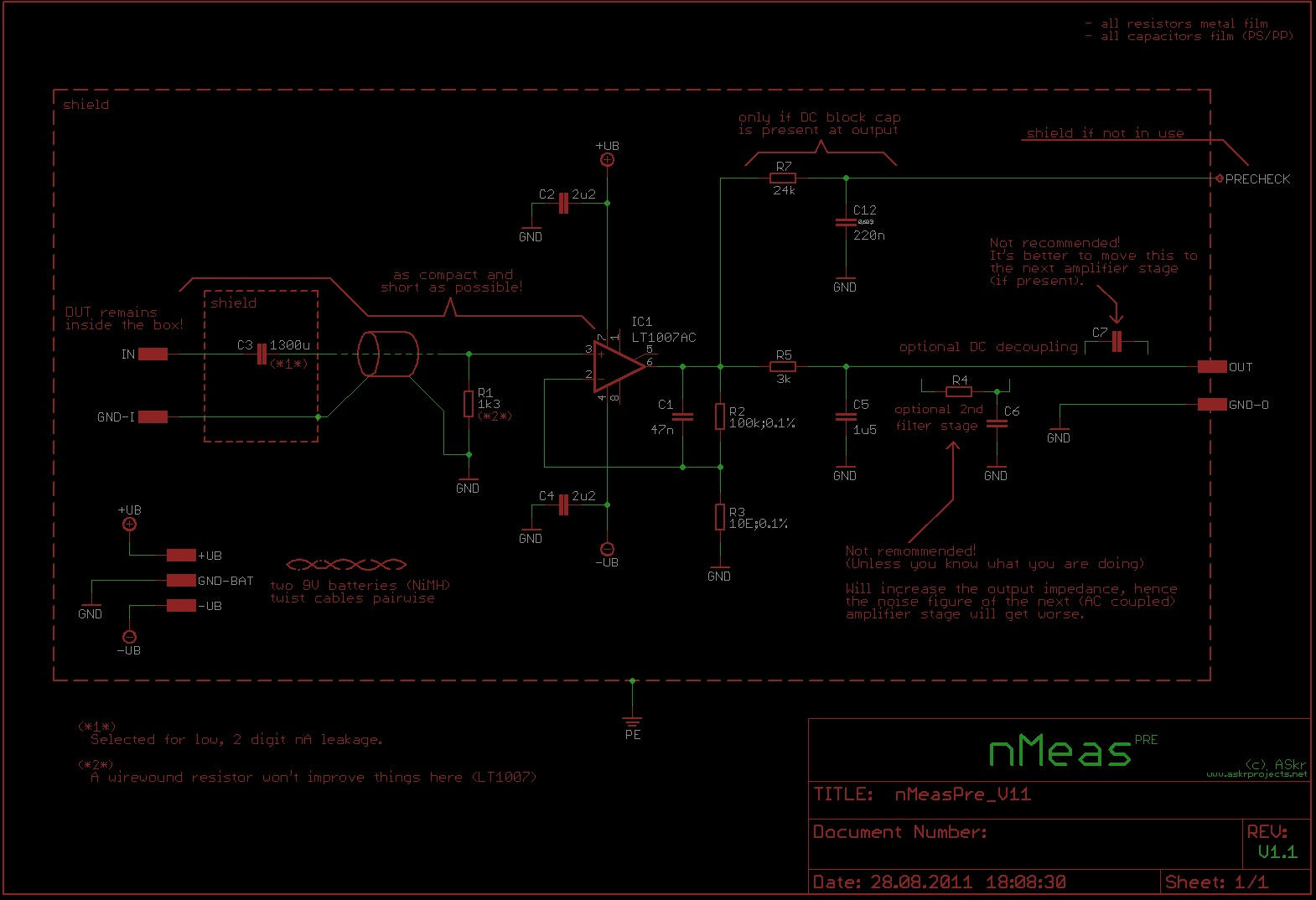
The nMeas-PRE amplifier is very sensitive and needs to reside in a shielded, grounded box.
The input signal first hits the C3/R1 combination, which decouples the DC component of the signal and additionally creates a high-pass filter (fc ≈ 0.94Hz).
Note: C3 is not a standard capacitor and requires the most attention.
The signal is then amplified by a factor of ~10'000 (~80dB, R2/R3) and finally passes
a ~35Hz low-pass filter (R5/C5).
In conjunction with C1, which limits the amplifier 3dB bandwidth to ~34Hz, the amplitude
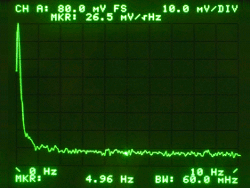
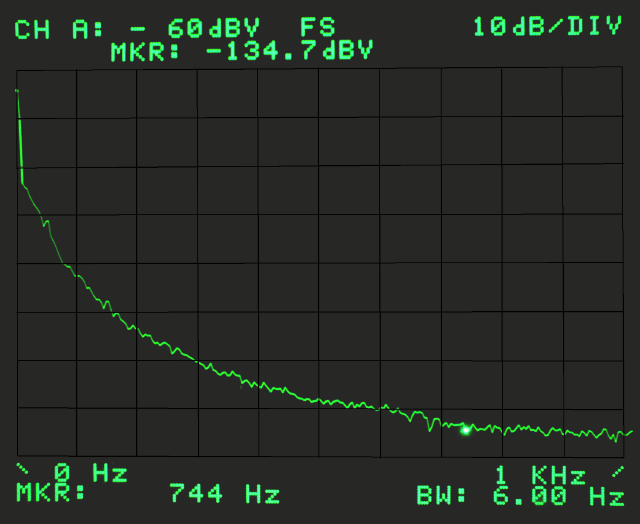
response drops ~40dB/decade above 30Hz (~50dB drop 10..744Hz; see right; at HP-3582A limit).
Due to dielectric absorption,
it will take hours and hours until the leakage current of the giant input capacitor drops
down to a minimum. If you decided to put the decoupling capacitor C7 inside the box, which is not
recommended, the "sneak-preview-tap" R7/C12, allows for checking the DC component of the
output signal. Disregarding any environmental influences and the 1/f noise contribution of the LT1007 (ultra-low fc ≈ 2Hz), a resistors noise power density can be calculated with: 
Or, more common, as voltage noise density: 
Because each noise source is independent of all others, they sum up in a square-sum-root fashion. 
At first, we set the input impedance as: 
With Av as gain, the output noise voltage density calculates to: 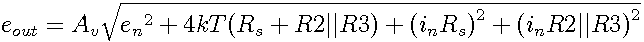
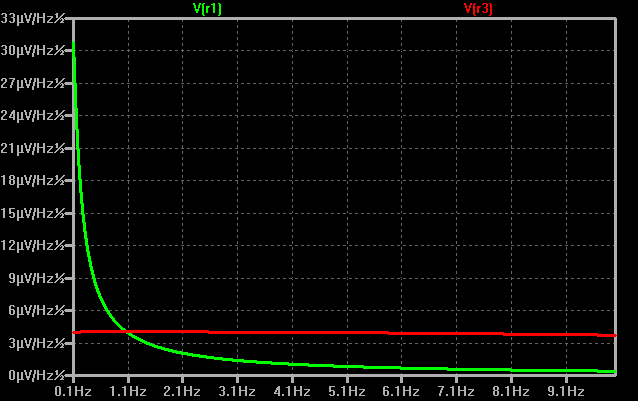
Skipping R2, because its decades above R3 and the resulting sum of R1+R2 won't be much larger than R1: 
the output noise estimation becomes 
Fortunately, this is not the end of the story. Only considering the above, the four terms would calculate to (worst case, using maximum voltage and current noise densities at 10Hz): 
While the last term (R3 current noise contribution) can be taken out, it is clear to see that
R1 dominates the noise figure. If you manage to find a capacitor >1300uF, with less than
20nA leakage current, decrease R1, but remember to fulfill the high-pass corner frequency requirement
( fc = 1/(2*PI*R1*C3); fc < 0.1Hz). For a detailed description on how to select an apropriate capacitor and why an extremely low leakage current is mandatory, see the next chapter. Now, after reducing the formula to 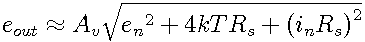
the approximate output voltage noise density (around 10Hz) will be 
The left image shows the actual real-world measurement. Marker is at 5Hz and reads ~75uV/sqrt(Hz).
But that is still not the complete story...
If a voltage source is attached to the input, its output impedance (Rv) appears in parallel to R1,
clamped together via C3. 
Notice that the formula above is not true for calculating the noise of the circuit!
For the ease of it, we assume an ideal voltage source (less math typesetting in LaTeX for me ;-) 
with 
And all together (except for the latter Xc; my fingers are tired of LaTeX math...) 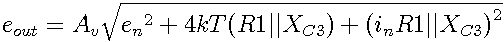
E.g., at f = 10Hz, we now have a new source impedance of Rs2 ≈ 12Ω. 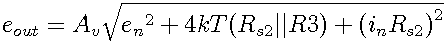
Compared to FIGURE B above, this value is far too large 
Why? Evaluating the three terms in the formula above reveals what happened: 
At least for this 10Hz approximation, now, the source impedance has almost no influence on the noise figure. And if we replace the worst case LT1007 settings by more typical values for the voltage noise density un=2.8nV/sqrt(Hz), we get comparable results: 
Additionally, with a source impedance as low as ~12Ω, now even R3 (10Ω, 410pV/sqrt(Hz), or 4.1uV/sqrt(Hz) at the output) need to be considered (but its noise is still 1/11 of the LT1007s contribution).
Below ~1Hz, the noise of the source impedance noticeably adds to the 1/f noise of the opamp.
Capacitor Selection
2nd stage amplifier (nMeas-AMP)
Sampling Unit (nMeas-???) |
Software
|
Acquisition
Analysis
Vrms <-> Vpp Conversion Notes |
Examples
|
Some Regulators
HP-3582A |
Some Useless Pics
(If you know what you are doing...)

Download
nMeas (1/f):
Includes:
- all you need
- ...
DOWNLOAD:
ASkr 08/2011: initial public release